3b1b Lec1: The simpler quadratic formula
My notes from 3blue1brown #1 lecture.
What is it?
This lecture is about deriving the quadratic formula in a more intuitive matter. For those of you who don’t remember, the quadratic formula is the formula $$ r, s = \frac{-b \pm \sqrt{b^2-4ac}}{2a}.$$ Here $r$ and $s$ is the roots of the function $f(x) = ax^2 + bx + c$. The roots $r$ and $s$ represents where on the $x$ axis $f(x) = 0.$ This is illustrated in the picture below:
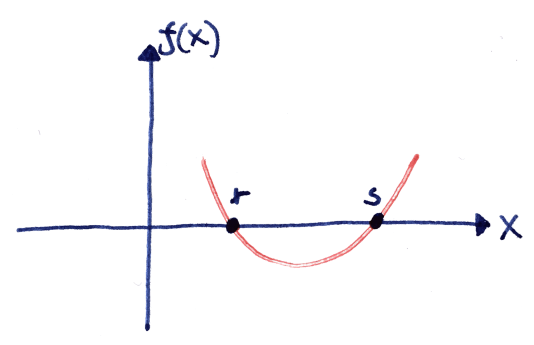
But where does this come from? This formula seems so arbitrary. Lets first take a small side tour and talk about primes (I promise it will be relevant).
Prime factorization
Let say you get asked to factorize $$35.$$ Some might fast reqognize that $$35 = 5\times7.$$ How about $143$? This would definitly take som more time. But eventually you might be able to deduce that $$143=11\times13.$$ But how about 3599? Impossible. Right? But there is a trick. This of course won’t work for all factorizations, but it is worth trying. Recognize that our previous numbers where almost equal to the sqare of some number. That is: $$6^2 = 36 \approx 35.$$ $$12^2 = 144 \approx 143.$$ By using the general formula: $x^2-1=(x+1)(x-1)$. If we take: $$6^2-1 = 35 = (6-1)(6+1) = 5\times7.$$ Just what we found before! Using this on 3599 we get: $$60^2-1 = 3599 =(60-1)(60+1) = 59\times61.$$ Here 59 and 61 happens to be primes! So we just factorized 3599. The take home message for this trick is to show the power of the formula $m^2-1=(m+1)(m-1)$. Which more generally can be written as: $$m^2-d^2=(m+d)(m-d).$$ Using that you can express any number, let’s call them $r$ and $s$ (not random naiming hehe), as some midpoint between those numbers and the distance from that midpoint to the number, this is actually really usefull to solve the quadratic formula.
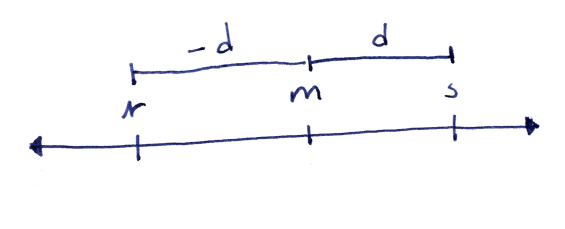
Solving the quadratic formula
We want to solve the equation $$ax^2+bx+c=0.$$ This might also be written as $$ \tag{1} x^2+\frac{b}{a}x+\frac{c}{a} = 0.$$ If we call the roots $r$ and $s$ the equation might also be written as $$\tag{2} (x-r)(x-s) = x^2 -(s+r)x+rs = 0.$$ Let us now introduce $m$ and $d$ as in the picture below. Notice that you can write $r=m-d$ and $s=m+d$.
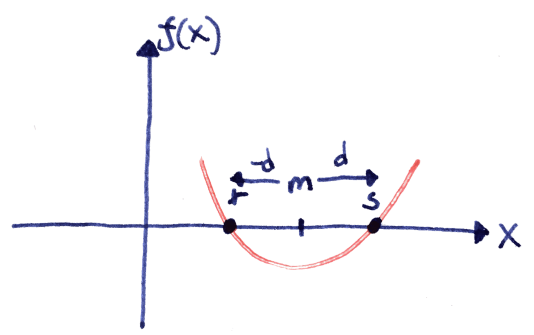
Now comparing equation 1 and 2 above we know three facts:
- $-(s+r) = \frac{b}{a}.$
- $rs = \frac{c}{a}.$
- $rs = (m-d)(m+d).$
You might recognize the third fact from our past prime factorization. So we can actually write this as $rs=m^2-d^2$. Let’s rewrite this further as $$d = \sqrt{m^2-rs}.$$ Now to compute this $d$ value we only need $m$, but $m$ is actually easy, it is by definition the middle point between $r$ and $s$, hence we can compute this as: $$m = \frac{s+r}{2}=\frac{-b}{2a}.$$ Here we used fact 1. Putting it all together: $$r,s = m \pm d = \frac{-b}{2a} \pm \sqrt{\frac{b^2}{4a^2}-\frac{c}{a}}.$$ Now with a little algebra this can be written as: $$ r, s = \frac{-b \pm \sqrt{b^2-4ac}}{2a}.$$