3b1b Lec2: Trigonometry fundamentals
My notes from 3blue1brown #2 lecture.
What is it?
This lecture is primary about becomming more familiar and comfartable with cosinus and sinus. First, let’s go over to desmos (https://www.desmos.com/calculator) and plot a graph. Let’s do $\cos(x)$. A question you might naturally ask next is how would $\cos(x)^2$ look like? (Who wouldn’t ask that question next?) If you think about it before plotting it is not at all trivial. I dare you to take a pencil and paper and sketch it out, then look if you got it right after in desmos.
In case you didn’t bother with desmos, here is a plot of $\color{red}{\cos(x)}$ and $\color{blue}{\cos(x)^2}$ for you.
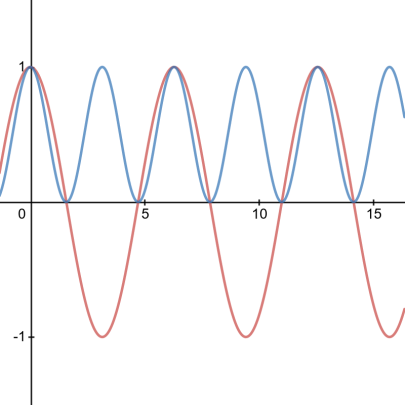
Now I at least think it is non-intuitive that the frequency doubles when you square $\cos(x)$. By looking at $\cos(x)$ you might see that if you add $1$ and multiply by $1/2$ you get something close to $\cos(x)^2$. Under you see $\color{red}{\frac{1}{2}(\cos(x)+1)}$ and $\color{blue}{\cos(x)^2}$.
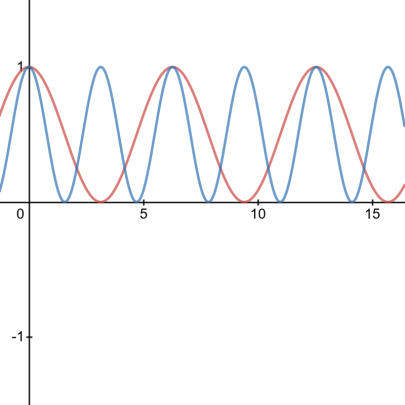
However you are still missing the doubling of the frequency, doing so results in the equality:
$$\cos(x)^2 = \frac{1}{2}(\cos(2x)+1).$$
By looking at this, I will say this is not at all trivial. This little investigaiton that we just did casts some light on the cosine function. We see that the cosine exhibits some same properties as exponents. That is, e.g.: $$(2^x)^2 = 2^{2x}.$$ We will come back to this, but for now, it is just a teaser.
Trigonometry basics
As som reddit user once said:
You think it’s about triangles, but really it’s about circles.
I think this sentence really sums up what trogometry is really about. Actually, a circle is embedded in the definition of $\cos(\theta)$. Here $\cos(\theta)$ is defined as the distance on the x-axis if you walk a distance $\theta$ around a circle of unit 1. See picure below.
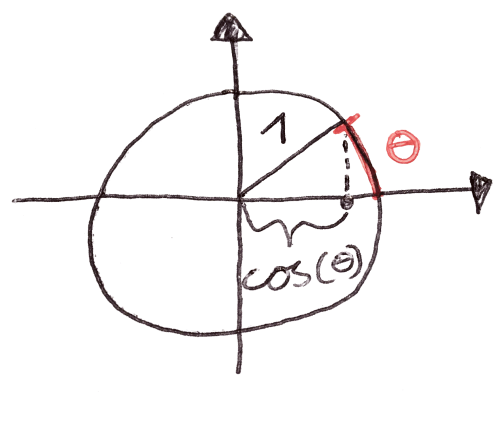
Here $\theta$ is measured in radians. Now a typically thing to learn from school is the rule: SohCahToa. This can be summed up by the picture below.
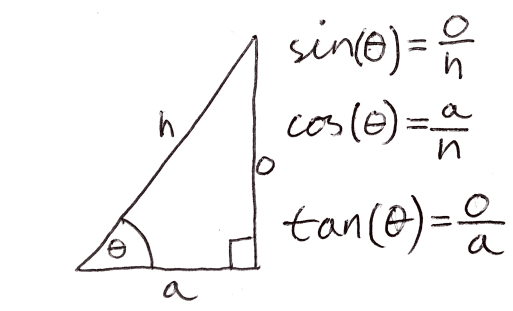
Now if we rearrange one of the equations to something like: $$h\cos(\theta)=a.$$ We se that we have the original definition of $\cos(\theta)$, but with a scaling factor $h$ since the circle is not necessarily 1. From the rules we see that $\sin(\theta)$ gives us $o$ or the distance on the y-axis. We can actually think of $\cos(\theta)$ and $\sin(\theta)$ as cordinates that traces a circle of radius 1. Let the picture below enlighten you!
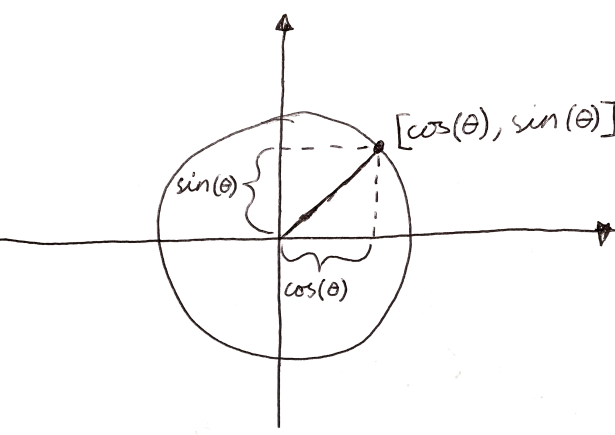
I will stop here for now. As this an important point for the next lesson: that $\sin(\theta)$ and $\cos(\theta)$ describes cordinates on a circle.