3b1b Lec3: Complex number fundamentals.
My notes from 3blue1brown #3 lecture.
Which numbers really exist?
$$2,\ \sqrt{2},\ -3,\ \sqrt{-1},\ \infty \ \text{?}$$
Does numbers exist at all? What do we mean when we say that something exists? Maybe for math, we can defined it as something that is usefull in the real world. Think about it, negative numbers wasn’t recognized as valid solution by mathemeticians in the start. But in the real world they can have a meaning, e.g. they can explain how much money I owe the bank.
This lesson will try to show that defining complex numbers can be meaningful in the real world.
By the end of this lesson you will be able to easly see that the properties below are correct: $$\cos(\alpha+\beta) = \cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)$$ $$\sin(\alpha+\beta) = \cos(\alpha)\sin(\beta)+\cos(\beta)\sin(\alpha)$$ Which I think is not at all easy by just looking at the equations. However this is easy with complex numbers. And even though you might still protest the fact that $\sqrt{-1}$ exists, you have to admit that it is interesting that believing it exist can make us easier understand certain areas of math.
Weird assumptions
Let us define a number $i^2=-1$. After this definition a typicall conversation would go something like:
“Wait, there is no such numbers!”
“But we just defined it.”
“…”
“You can do that? Just define solutions?”
Well, you can actually define solutions to equations, you of course have to make sure the definition dosn’t contradict previous definitions, e.g. you cannot just define $5=1$. When doing such definitions, like $i^2=-1$ you should also make sure you define how operations with the definition works. So lets do that.
Addition
$$(a+bi) + (c+di) = (a+c)+(b+d)i$$
Multiplication
$$i(a+bi) = ia + bi^2 = -b+ai$$
Now we will define one more thing. We will define that $i$ lies in another dimension than the real numbers. Gemoetrically this means that we can think of $i$ as an axes perpendicular to the real numbers. This definition, together with the definition of multiplication, reveals that multiplying some complex number by $i$ rotates that number by $90^{\circ}$. See picture below.
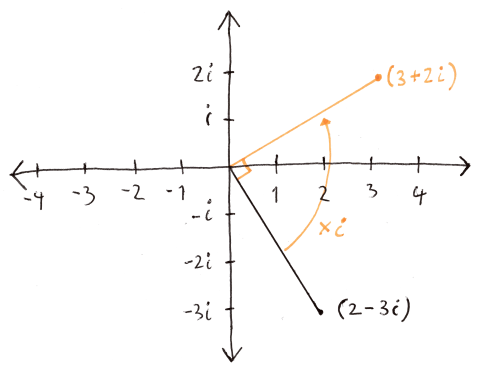
3 facts about multiplication
- $$Z \times 1 = Z$$
- $$Z \times i = \text{Rot90}^{\circ}(Z)$$
- $$Z \times (c+di) = c\times Z + d\times (Zi)$$
The third one is interresting. As the last part is just a scaled version of the 90^{\circ} rotatet $Z$, and the first part is just a scaled version of $z$. The multiplication of two comoplex numbers can be illustrated as below